With this application, you can:

• Compress images with this fractal method
• Decompress previously compressed images into a different format

Make use of the platform's libraries, which include the following features:

• Multi-language
• Configurable multi-resolution zoom
• Dark mode option
• New version notification

Pros:

• When properly programmed, it functions independently of the image resolution
• It is a distinctive compression method
• Allows you to learn as you go

Cons:

• The compression process is extremely slow
• You don't achieve very high compression ratios (at least with the parameters I used)

It's an implementation of this fractal image compression algorithm published in IEEE during my college days

The application utilizes the Delaunay incremental triangulation library, which is also used in the Morphing application

High-level algorithm:

• Compression:
  • Fractal compression focuses on storing relationships between image regions rather than the actual pixel values, specifically between triangles in this case.
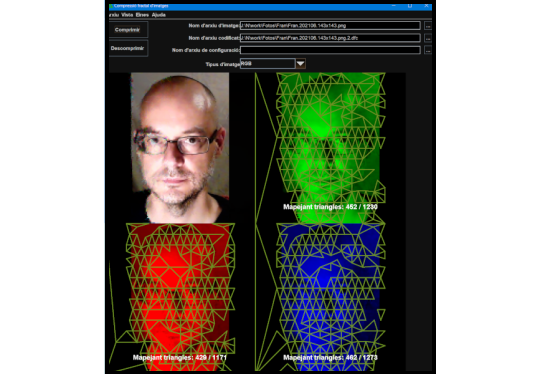
  • The image is divided into a triangular grid consisting of multiple triangles, forming a triangulated domain.
  • The image is subdivided into a new set of triangulations featuring larger triangles designated for the codebook.
  • The triangulations are dynamic, and the split and merge algorithm is applied based on the variance of the triangle pixels.
  • Once the triangulation for the codebook is determined, the most representative 2^n triangles are selected to form the codebook. The value of n significantly impacts the compression time while having a minor effect on the compression ratio and the quality achieved.
  • For each domain triangle, the optimal mapping with a triangle from the codebook is sought using a minimum mean square error (MSE) criterion
  • The optimal mapping between triangles is found by making combinations of::
    • Permutations of the vertices (6 possibilities)
    • Determining an offset for the mean
    • Finding a scale factor between 0 and 1, which is applied to the deviation from the mean. This scale factor should remain between 0 and 1 to prevent divergence during the iterative decompression process
    Additionally, these parameters should be quantized using a limited number of bits to ensure that both the compression time and ratio are reasonable and in line with the desired quality.
• The stored information in the compressed file for each channel:
  • The information to reproduce the two triangulations:
    • Triangles that split in each iteration
    • Vertices that were removed as a result of the merge (after completing the split iterations)
  • The selection of the 2^n triangles of the codebook
  • The optimal mapping of each domain triangle:
    • Which codebook triangle it uses to map (n bits)
    • The optimal vertex permutation (6 combinations, 3 bits)
    • Offset (the authors indicate that the offset is effectively represented with 6 bits)
    • Scale (the authors indicate that the scale is effectively represented with 6 bits)
• Decompression (for each channel):
  • The triangles of the two triangulations are obtained.
  • The codebook triangles are obtained.
  • This process is repeated until convergence is achieved:
    • The mapping of all domain triangles to their optimal correspondences with the codebook triangles

After earning a Master's degree in Artificial Intelligence, I envision innovating how to derive the most significant triangles for the codebook by applying K-medoids.

I am unsure if the innovation will improve or hinder the algorithm, but it saves me from needing to program it myself, which initially seemed complicated.

Image processing is divided into channels, typically RGB.

It utilizes multiprocessing, with one thread dedicated to each channel.