The library enables the application of a lens effect to a Java Swing JPanel
For version v1.2, I created a demo application that displays the lens on a JFrame, which can be dragged across the entire screen
I created the lens effect to provide an engaging feature for the "About" section of the file encryption application
The library enables the application of a lens effect to a Java Swing JPanel
For version v1.2, I created a demo application that displays the lens on a JFrame, which can be dragged across the entire screen
The lens effect is created using a polar coordinate transformation, where the angle stays the same, and the radius is elongated near the center while being compressed towards the edges. The radius remains unchanged at the center and edges
A Gaussian smoothing filter with a size of 3x3 is then applied


The small application lens effect was the by-product of a spring break with no plans.
At that time, I was finishing programming the first version of the encoder (File Encoder Application), and I needed something catchy for the About ...
The original idea is not mine, but I implemented it based on an effect I had seen in one of those iconic DOS demos.
I decided to encapsulate the effect within a Java Swing JPanel for my project.
Everything within the panel can be magnified using a magnifying glass positioned at your chosen coordinates.
It was especially challenging to ensure that refreshing the text components, especially when modifying the selected text's location, did not adversely affect the visual appearance.
When you create the LensJPanel, the content of the JPanel is applied to the element that will undergo the magnifying effect. You can specify the radius of the magnifying glass and whether it will magnify or diminish the content.
When you have the radius and determine whether the magnifying glass will enlarge or shrink the content, a two-dimensional square matrix is created with one element for each square pixel containing the magnifying glass.
The algorithm calculates the coordinates of the corresponding source pixel in the original image for each destination pixel to determine the color when applying the transformation.
The transformation involves a simple polar coordinate transformation, which is why a magnifying lens is utilized:
A pixel is calculated from a specific position of the lens frame and is used to determine the color when the transformation is applied. The pixel will also be within the lens frame. In addition, the radius from the center of the lens to the angle for a given pixel is calculated. The "origin" pixel for the pixel we are calculating will be at the same angle, but the radius will change. The radius spans from 0% to 100% for both the “target” and “source” pixels, with 100% representing the length of the lens radius. The source pixel is calculated for each target pixel by maintaining its angle and transforming the radius using a function with a monotonically increasing derivative. This transformation occurs in the interval between 0 and 1, where f(0) equals 0 and f(1) equals 1. Here, 0 represents 0% of the lens radius, and 1 represents 100% of the lens radius. This means that the radii will take their source pixel from a smaller radius, which will expand the lens circle. Outside the circle of the lens, the transformation will be the identity, meaning the source pixel will not change.
The explanation is a bit confusing, but if you are interested in learning more about the subject, feel free to contact me.
I hope someone will find it useful :-).
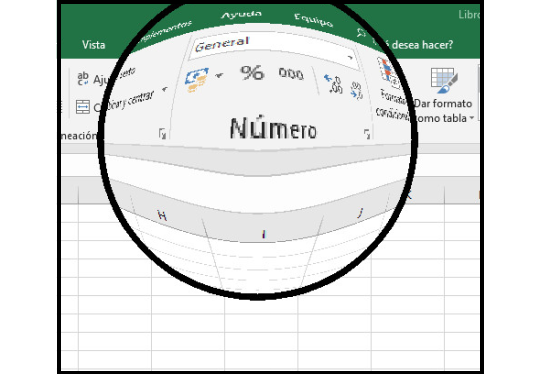
The application's new version features a circular graphic window with a movable lens that can be controlled by clicking and dragging with your mouse.
You can exit the application by pressing ESC.
A couple of problems are evident:
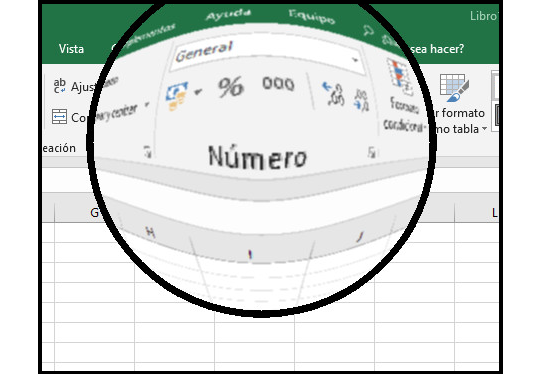
The new version of the application addresses a transparency bug that occurred on Mac and Linux operating systems.
The latest version also addresses the pixelation issue found in previous versions.
This is accomplished by applying a Gaussian smoothing filter to the lens image, creating a blurring effect that reduces the pixelation caused by magnification.
The latest available subversion of this version works with both Java-8 and Java-11.

