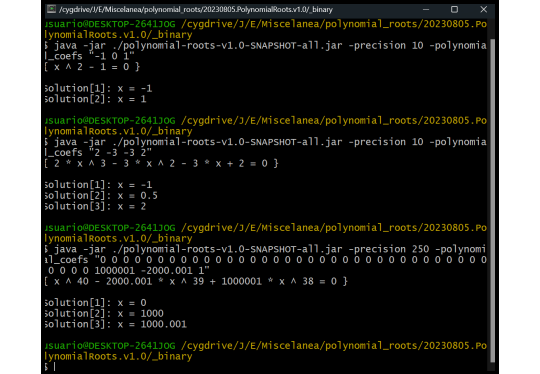
The command line application accepts polynomial coefficients and a precision parameter, calculating the polynomial's real zeros.
Windows
Polynomial Roots (2023)
DownloadThe application was created to solve the problem of calculating the real roots of a given polynomial in a unique way
The command line application accepts polynomial coefficients and a precision parameter, calculating the polynomial's real zeros.
Command line Java application.
The concept of this algorithm involves the following steps:
However, there's a catch-22: We must first compute the zeros of the derivative function in order to define the zeros of the polynomial itself!
Solution: We apply recursion until we reach a polynomial that allows easy calculation of its zeros. This process can be repeated until we derive an affine function
Disadvantages:
For realistic degrees found in real life, there should be no problem
The algorithm has been designed without assuming any floating-point data, utilizing Java generics instead
The application supports the use of Double or BigDecimal, but a Float version could easily be implemented
It is a proof of concept. Programming it for BigDecimal alone would have sufficed, but using generics makes the algorithms cooler and more illustrative for beginners
I haven't extensively tested the application yet, and there's a possibility it could be fine-tuned to improve accuracy and functionality in more scenarios. However, I believe the code has great potential.
I think it can be effectively adjusted to work in all scenarios.


Polynomial root calculators are a staple in the field of computer science careers.
I contribute my version of the solution to the problem.
It is not a very efficient solution since the computational complexity in the worst case is O(G^2), where G represents the polynomial degree
However, I think it gets the job done effectively
The algorithm is based on calculating the roots of a polynomial, assuming that the roots of its derivative function are known
Under this assumption, it is straightforward to calculate the roots because we can determine the range limit of the roots (See: Properties of the polynomial roots)
In this manner, we can determine the range of each potential root by using the derivative function roots, and we can compute the zeros by applying Bolzano's theorem.
But ... we need the function to calculate the roots of the derivative function!
No problem. We use recursion to compute the roots of a polynomial. The recursive function has a termination case for the scenario of a polynomial of degree zero (a constant), which we assume has no roots.
Since the derivative function has one degree less than the original polynomial, by using recursion, we can calculate the roots of a polynomial at zero degrees, making it a simple problem to solve
This way of proceeding may require precision in our calculations, but that is not a problem if we use the Java BigDecimal class.
