La aplicación (de línea de comandos), acepta los coeficientes de los polinomios, y una precisión para los cálculos, y calcula los ceros reales del polinomio.
Pantallas
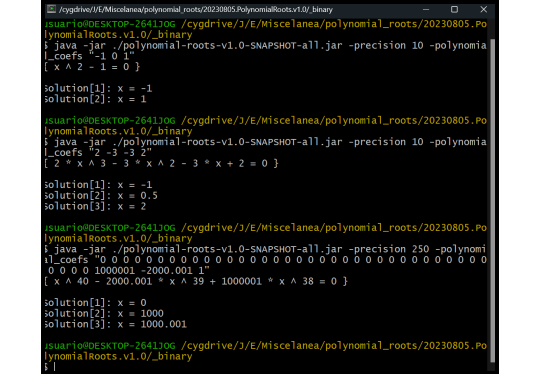
Raíces de polinomios (2023)
DescargarLa aplicación nace con el deseo de solucionar "a mi manera", el problema del cálculo de las raíces reales de un polinomio dado
La aplicación (de línea de comandos), acepta los coeficientes de los polinomios, y una precisión para los cálculos, y calcula los ceros reales del polinomio.
Aplicación Java de línea de comandos.
La idea del algoritmo es esta:
Pero parece una pescadilla que se muerde la cola! Necesitamos calcular los ceros de la función derivada para delimitar los ceros de nuestro polinomio!
Pues fácil: Aplicamos recursividad, hasta llegar a un polinomio que se pueda calcular fácilmente los ceros (puede derivarse reiteradamente, hasta llegar a una función afín)
Desventajas:
Pero para grados razonables que nos podemos encontrar en la vida real, no debería de haber problema
El algoritmo se ha programado sin presuponer ningún tipo de datos de coma flotante (está expresado con los generics de Java)
La aplicación permite hacer uso de Double o BigDecimal, pero podría implementarse fácilmente una versión para Float
Es una prueba de concepto ... En realidad hubiera bastado con programarlo para BigDecimal, pero los algoritmos con generics molan más, y pueden ser ilustrativos para los que empiezan
La aplicación no ha sido probada exhaustivamente, y quizás pueda tunearse un poco más para que sea más precisa o funcione en más casos, pero creo que el código tiene muchas posibilidades.
Creo que puede tunearse convenientemente para que funcione en todos los casos.


Las calculadoras de raíces de polinomios son un clásico en las carreras de informática.
Contribuyo con mi versión de la solución al problema.
No es una solución muy eficiente, ya que en el peor caso la complejidad computacional es O(G^2), siendo G el grado del polinomio
Pero creo que hace el trabajo con efectividad
El algoritmo se basa en el cálculo de las raíces de un polinomio, suponiendo conocidas las raíces de su función derivada
Bajo esa suposición, es muy sencillo calcular las raíces, ya que podemos conocer el límite del rango donde se encuentran todas las raíces (Véase: Propiedades de las raíces polinómicas)
Y de esta manera, en combinación con las raíces de la función derivada, podemos delimitar el rango de cada una de las posibles raíces y, simplemente aplicando el teorema de Bolzano, podemos calcular los ceros
Pero ... necesitamos la función que estamos programando para calcular las raíces de la función derivada!
No hay problema: usamos recursividad, y la función recursiva (la que calcula las raíces de un polinomio), tiene un caso de terminación para el caso de un polinomio de grado cero (una constante), que supondremos que no tiene raíces.
Como la función derivada tiene un grado menos que el polinomio original entonces, aplicando la recursividad, llegaremos al cálculo de las raíces de un polinomio de grado cero, con solución trivial y problema solucionado
Esta manera de proceder puede crear la necesidad de tener alta precisión en los cálculos, pero eso no es problema si usamos la clase BigDecimal de Java
